前言
如果你已经阅读并贯彻了之前关于Transformer的文章Transformers, can you rate the complexity of reading passages? 这意味着你已经熟悉了Transformer的基本原理或训练过程以及Transformer微调或训练过程的基本知识。
如果我的Transformer的性能没有达到你的预期,我能做什么?可以尝试超参数的调整。此外,也可以尝试实现一些高级训练技术,我将在这篇文章中介绍这些技术。这些技术可用于微调变形器,如BERT、ALBERT、RoBERTa和其他。
主要内容
- Layer-wise Learning Rate Decay (LLRD)
- Warm-up Steps
- Re-initializing Pre-trained Layers
- Stochastic Weight Averaging (SWA)
- Frequent Evaluation
- Results
- Summary
对于我们在这篇文章中要做的所有高级微调技术,我们将使用与Transformers, can you rate the complexity of reading passages?一文种一致的模型。
最后,我们将能够比较基本微调的结果和应用高级微调技术得到的结果。
1.Layer-wise Learning Rate Decay (LLRD)
在Revisiting Few-sample BERT Fine-tuning中,作者将分层学习率衰减描述为
“a method that applies higher learning rates for top layers and lower learning rates for bottom layers. This is accomplished by setting the learning rate of the top layer and using a multiplicative decay rate to decrease the learning rate layer-by-layer from top to bottom”.
“一种方法,它为顶层应用更高的学习率,为底层应用更低的学习率。这是通过设置顶层的学习率并使用乘法衰减率从顶部到底部逐层减少学习率来实现的。”
类似的概念称为区分微调,也在通用语言模型微调中用于文本分类(Universal Language Model Fine-tuning for Text Classification)。
“Discriminative fine-tuning allows us to tune each layer with different learning rates instead of using the same learning rate for all layers of the model”
“区分微调允许我们使用不同的学习率调整每个层,而不是为模型的所有层使用相同的学习率”
所有这些都是有道理的,因为Transformer模型中的不同层通常捕获不同类型的信息。底层通常编码更常见,更广泛和基于广泛的信息,而靠近输出的顶层编码更局部和特定于手头的任务的信息。
在我们进入实现之前,让我们快速回顾一下我们为Transformers所做的基本微调Transformers, can you rate the complexity of reading passages?在一个由一个嵌入层和12个隐藏层组成的roberta-base模型上,我们使用了一个线性调度器,并在优化器中设置了一个初始学习率为1e-6(即0.000001)。如下图所示,调度器创建了一个学习率的时间表,在训练步骤中,该学习率从1e-6线性减少到零。
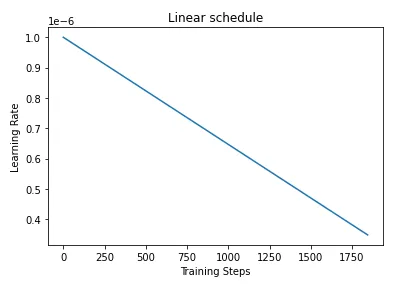
实现分层学习率衰减(或区分微调)有两种可能的方法。
第一种方法是遵循Revisiting Few-sample BERT Fine-tuning中描述的方法。我们选择3.5e-6的学习率用于顶层,并使用0.9的乘性衰减率,从顶部到底部逐层减少学习率。这将导致底层(嵌入和layer0)的学习率大致接近于1e-6。我们在一个名为roberta_base_AdamW_LLRD的函数中执行此操作。
好的,我们已经设置了隐藏层的学习率。那么池化器和回归器头部呢?对于它们,我们选择了3.6e-6的学习率,略高于顶层。
在下面的代码中,head_params、layer_params和embed_params是定义我们要优化的参数、学习率和权重衰减的字典。所有这些参数组都传递到AdamW优化器中,该优化器由函数返回。
def roberta_base_AdamW_LLRD(model):
opt_parameters = [] # To be passed to the optimizer (only parameters of the layers you want to update).
named_parameters = list(model.named_parameters())
# According to AAAMLP book by A. Thakur, we generally do not use any decay
# for bias and LayerNorm.weight layers.
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
init_lr = 3.5e-6
head_lr = 3.6e-6
lr = init_lr
# === Pooler and regressor ======================================================
params_0 = [p for n,p in named_parameters if ("pooler" in n or "regressor" in n)
and any(nd in n for nd in no_decay)]
params_1 = [p for n,p in named_parameters if ("pooler" in n or "regressor" in n)
and not any(nd in n for nd in no_decay)]
head_params = {"params": params_0, "lr": head_lr, "weight_decay": 0.0}
opt_parameters.append(head_params)
head_params = {"params": params_1, "lr": head_lr, "weight_decay": 0.01}
opt_parameters.append(head_params)
# === 12 Hidden layers ==========================================================
for layer in range(11,-1,-1):
params_0 = [p for n,p in named_parameters if f"encoder.layer.{layer}." in n
and any(nd in n for nd in no_decay)]
params_1 = [p for n,p in named_parameters if f"encoder.layer.{layer}." in n
and not any(nd in n for nd in no_decay)]
layer_params = {"params": params_0, "lr": lr, "weight_decay": 0.0}
opt_parameters.append(layer_params)
layer_params = {"params": params_1, "lr": lr, "weight_decay": 0.01}
opt_parameters.append(layer_params)
lr *= 0.9
# === Embeddings layer ==========================================================
params_0 = [p for n,p in named_parameters if "embeddings" in n
and any(nd in n for nd in no_decay)]
params_1 = [p for n,p in named_parameters if "embeddings" in n
and not any(nd in n for nd in no_decay)]
embed_params = {"params": params_0, "lr": lr, "weight_decay": 0.0}
opt_parameters.append(embed_params)
embed_params = {"params": params_1, "lr": lr, "weight_decay": 0.01}
opt_parameters.append(embed_params)
return transformers.AdamW(opt_parameters, lr=init_lr)
下面是一个具有分层学习率衰减的线性调度器的示例:
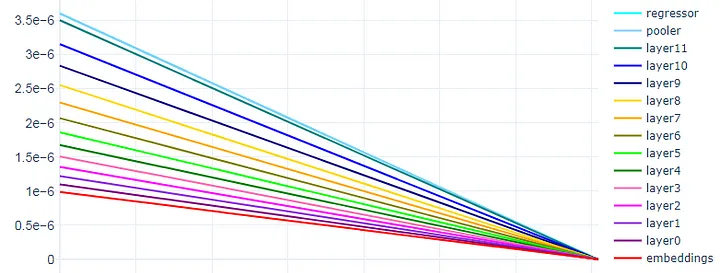
第二种实现分层学习率衰减(或区分微调)的方法是将层分组到不同的集合中,并对每个集合应用不同的学习率。我们将其称为分组LLRD。
使用一个名为roberta_base_AdamW_grouped_LLRD的新函数,我们将roberta-base模型的12个隐藏层分成3组,其中嵌入附加到第一组。
下面是一个具有分组LLRD的线性调度器的示例:
- Set 1 : Embeddings + Layer 0, 1, 2, 3 (learning rate: 1e-6)
- Set 2 : Layer 4, 5, 6, 7 (learning rate: 1.75e-6)
- Set 3 : Layer 8, 9, 10, 11 (learning rate: 3.5e-6)
与第一种方法相同,我们使用3.6e-6作为池化器和回归器头部的学习率,略高于顶层。
def roberta_base_AdamW_grouped_LLRD(model):
opt_parameters = [] # To be passed to the optimizer (only parameters of the layers you want to update).
named_parameters = list(model.named_parameters())
# According to AAAMLP book by A. Thakur, we generally do not use any decay
# for bias and LayerNorm.weight layers.
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
set_2 = ["layer.4", "layer.5", "layer.6", "layer.7"]
set_3 = ["layer.8", "layer.9", "layer.10", "layer.11"]
init_lr = 1e-6
for i, (name, params) in enumerate(named_parameters):
weight_decay = 0.0 if any(p in name for p in no_decay) else 0.01
if name.startswith("roberta_model.embeddings") or name.startswith("roberta_model.encoder"):
# For first set, set lr to 1e-6 (i.e. 0.000001)
lr = init_lr
# For set_2, increase lr to 0.00000175
lr = init_lr * 1.75 if any(p in name for p in set_2) else lr
# For set_3, increase lr to 0.0000035
lr = init_lr * 3.5 if any(p in name for p in set_3) else lr
opt_parameters.append({"params": params,
"weight_decay": weight_decay,
"lr": lr})
# For regressor and pooler, set lr to 0.0000036 (slightly higher than the top layer).
if name.startswith("regressor") or name.startswith("roberta_model.pooler"):
lr = init_lr * 3.6
opt_parameters.append({"params": params,
"weight_decay": weight_decay,
"lr": lr})
return transformers.AdamW(opt_parameters, lr=init_lr)
下面是一个具有分组LLRD的线性调度器的示例:
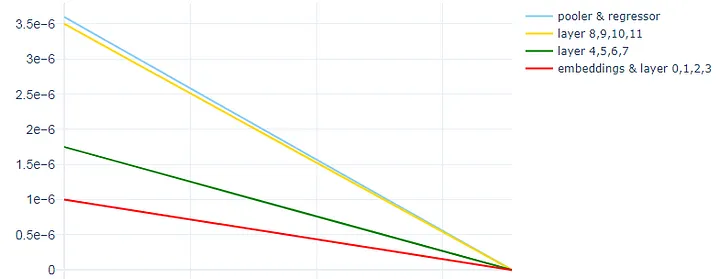
2. Warm-up Steps
对于我们使用的线性调度程序,我们可以应用热身步骤。例如,应用50个热身步骤意味着学习率将在前50个步骤(热身阶段)期间从0线性增加到优化器中设置的初始学习率。之后,学习率将开始线性降低到0。
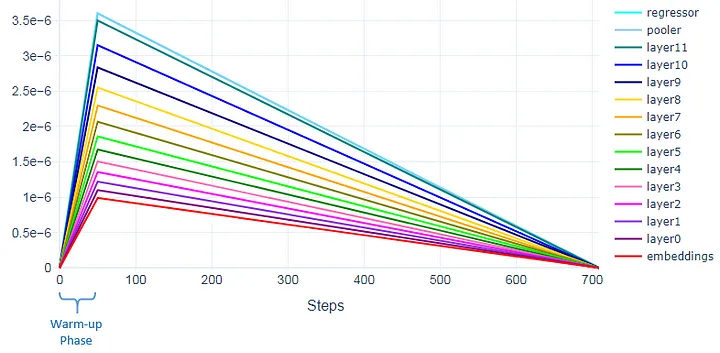
下图显示了第50步的相应层的学习率。这些是我们为优化器设置的学习率。
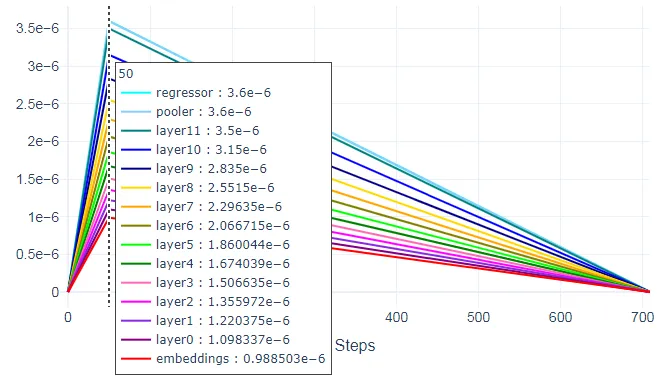
要应用热身步骤,请在get_scheduler函数上输入num_warmup_steps参数。
scheduler = transformers.get_scheduler(
"linear",
optimizer = optimizer,
num_warmup_steps = 50,
num_training_steps = train_steps
)
或者,您也可以使用get_linear_schedule_with_warmup。
scheduler = transformers.get_linear_schedule_with_warmup(
optimizer = optimizer,
num_warmup_steps = 50,
num_training_steps = train_steps
)
3. Re-initializing Pre-trained Layers
“Fine-tuning Transformer”是一种简单的方法,因为我们使用的是预训练模型。这意味着我们不是从头开始训练模型,这可能需要大量的资源和时间。这些模型通常已经在大量的文本数据上进行了预训练,并且它们包含了我们可以使用的预训练权重。但是,为了获得更好的微调结果,有时我们需要在微调过程中丢弃其中一些权重并重新初始化它们。
那么我们该如何做呢?早些时候,我们谈到了Transformer的不同层捕捉不同类型的信息。底层通常编码更通用的信息。这些信息很有用,因此我们希望保留这些低级别的表示。我们想要刷新的是靠近输出的顶层。它们是编码与预训练任务更相关的信息的层,现在我们希望它们适应我们的任务。
我们可以在之前创建的MyModel类中执行此操作。在初始化模型时,我们传递一个参数,指定要重新初始化的前n层。您可能会问,为什么是n?事实证明,选择n的最佳值至关重要,可以导致更快的收敛。也就是说,要重新初始化多少个顶层?好吧,这取决于每个模型和数据集的不同。对于我们的情况,n的最佳值为5。如果重新初始化超过最佳点的更多层,您可能会开始遇到恶化的结果。
如下所示,我们使用均值为0和由模型的initializer_range定义的标准偏差重新初始化nn.Linear模块的权重,并使用值为1的值重新初始化nn.LayerNorm模块的权重。偏差以0的值重新初始化。
如代码所示,我们还重新初始化了pooler层。如果您的模型中没有使用pooler,则可以在_do_reinit中省略与其相关的部分。
class MyModel(nn.Module):
def __init__(self, reinit_n_layers=0):
super().__init__()
self.roberta_model = RobertaModel.from_pretrained('roberta-base')
self.regressor = nn.Linear(768, 1)
self.reinit_n_layers = reinit_n_layers
if reinit_n_layers > 0: self._do_reinit()
def _do_reinit(self):
# Re-init pooler.
self.roberta_model.pooler.dense.weight.data.normal_(mean=0.0, std=self.roberta_model.config.initializer_range)
self.roberta_model.pooler.dense.bias.data.zero_()
for param in self.roberta_model.pooler.parameters():
param.requires_grad = True
# Re-init last n layers.
for n in range(self.reinit_n_layers):
self.roberta_model.encoder.layer[-(n+1)].apply(self._init_weight_and_bias)
def _init_weight_and_bias(self, module):
if isinstance(module, nn.Linear):
module.weight.data.normal_(mean=0.0, std=self.roberta_model.config.initializer_range)
if module.bias is not None:
module.bias.data.zero_()
elif isinstance(module, nn.LayerNorm):
module.bias.data.zero_()
module.weight.data.fill_(1.0)
def forward(self, input_ids, attention_mask):
raw_output = self.roberta_model(input_ids, attention_mask, return_dict=True)
pooler = raw_output["pooler_output"] # Shape is [batch_size, 768]
output = self.regressor(pooler) # Shape is [batch_size, 1]
return output
4. Stochastic Weight Averaging (SWA)
Stochastic Weight Averaging (SWA) 是一种深度神经网络训练技术,由 Averaging Weights Leads to Wider Optima and Better Generalization 提出。
“SWA is extremely easy to implement and has virtually no computational overhead compared to the conventional training schemes”
“SWA非常容易实现,与传统的训练方案相比,几乎没有计算开销”。
那么,SWA是如何工作的呢?
如 PyTorch 博客所述,SWA由两个部分组成:
-
首先,它使用修改后的学习率计划。例如,我们可以在前75%的训练时间内使用标准的衰减学习率策略(例如我们正在使用的线性计划),然后将学习率设置为合理的高常数值,以在剩余的25%的时间内进行训练。
-
其次,它采用网络遍历的权重的平均值。例如,我们可以在训练时间的最后25%内保持权重的运行平均值。训练完成后,我们将网络的权重设置为计算出的 SWA 平均值。
如何在 PyTorch 中使用 SWA?在
torch.optim.swa_utils中,我们实现了所有 SWA 部分,以便使用任何模型方便地使用 SWA。特别地,我们为 SWA 模型实现了
AveragedModel类,SWALR学习率调度程序和update_bn实用程序函数,以在训练结束时更新 SWA 批归一化统计信息。Source: PyTorch blog
SWA 在 PyTorch 中易于实现。您可以参考 PyTorch 文档中提供的示例代码来实现 SWA。您可以在这个 PyTorch 博客和这个 PyTorch 文档中了解有关 SWA 的更多详细信息。
loader, optimizer, model, loss_fn = ...
swa_model = torch.optim.swa_utils.AveragedModel(model)
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=300)
swa_start = 160
swa_scheduler = SWALR(optimizer, swa_lr=0.05)
for epoch in range(300):
for input, target in loader:
optimizer.zero_grad()
loss_fn(model(input), target).backward()
optimizer.step()
if epoch > swa_start:
swa_model.update_parameters(model)
swa_scheduler.step()
else:
scheduler.step()
# Update bn statistics for the swa_model at the end
torch.optim.swa_utils.update_bn(loader, swa_model)
# Use swa_model to make predictions on test data
preds = swa_model(test_input)
为了在我们的 run_training 函数中实现 SWA,我们需要传递一个 swa_lr 参数。这个参数是 SWA 学习率,设置为一个常数值。在我们的情况下,我们将使用 2e-6 作为 swa_lr。
因为我们想要在第 3 个 epoch 切换到 SWA 学习率调度并开始收集参数的 SWA 平均值,我们将 3 分配给 swa_start。
对于每个 fold,我们初始化 swa_model 和 swa_scheduler,以及数据加载器、模型、优化器和调度程序。``swa_model` 是累积权重平均值的 SWA 模型。
接下来,我们循环遍历 epoch,调用 train_fn 并将 swa_model、swa_scheduler 和一个布尔指示器 swa_step 传递给它。它是一个指示器,告诉程序在第 3 个 epoch 切换到 swa_scheduler。
from torch.optim.swa_utils import AveragedModel, SWALR
def run_training(df, model_head="pooler", ...., swa_lr):
swa_start = 3
....
....
for fold in FOLDS:
train_data_loader = ....
model = MyModel(reinit_n_layers=5).to(device)
optimizer, _ = roberta_base_AdamW_LLRD(model)
scheduler = transformers.get_scheduler(....)
swa_model = AveragedModel(model).to(device)
swa_scheduler = SWALR(optimizer, swa_lr=swa_lr)
....
....
for epoch in range(EPOCHS):
train_losses, ... = train_fn(train_data_loader, model, optimizer, ....,
swa_model, swa_scheduler,
True if swa_lr is not None and (epoch>=swa_start) else False)
....
....
torch.optim.swa_utils.update_bn(train_data_loader, swa_model)
....
....
在 train_fn 中,从 run_training 函数传递的 swa_step 参数控制了切换到 SWALR 和更新平均模型 swa_model 的参数。
def train_fn(data_loader, model, optimizer, ...., swa_step=False):
model.train() # Put the model in training mode.
....
....
for batch in data_loader: # Loop over all batches.
....
....
optimizer.zero_grad() # To zero out the gradients.
outputs = model(ids, masks).squeeze(-1) # Predictions from 1 batch of data.
....
....
loss.backward() # To backpropagate the error (gradients are computed).
optimizer.step() # To update parameters based on current gradients.
....
....
if swa_step:
swa_model.update_parameters(model) # To update parameters of the averaged model.
swa_scheduler.step() # Switch to SWALR.
else:
scheduler.step() # To update learning rate.
return train_losses, ....
SWA 的好处在于我们可以将其与任何优化器和大多数调度程序一起使用。在我们的线性调度中,使用 LLRD,我们可以从下图中看到,在第 3 个 epoch 切换到 SWA 学习率调度后,学习率保持在 2e-6 的常数。

下面是在具有 50 个热身步骤的分组 LLRD 上实现 SWA 后线性调度的样子:
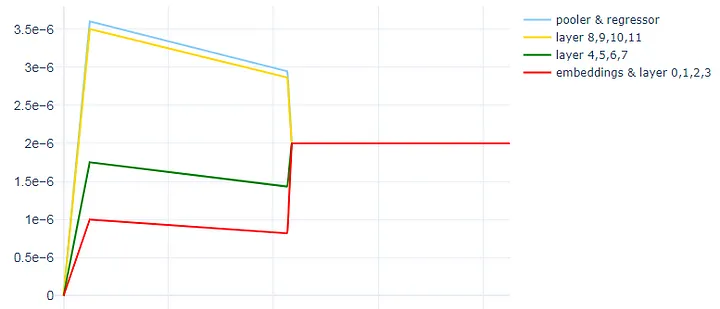
你可以在这个 PyTorch 博客和这个 PyTorch 文档中阅读更多关于 SWA 的细节。
5. Frequent Evaluation
频繁的评估是另一种值得探索的技术。它的意思是,我们不再在每个时期上进行一次验证,而是在时期内的每个x批次的训练数据上执行验证。这将需要我们在代码中进行一些结构更改,因为目前的训练和验证函数是分开的,并且每个时期都会调用两者一次。
我们将创建一个新函数train_and_validate。对于每个时期,run_training将调用此新函数,而不是分别调用train_fn和validate_fn。
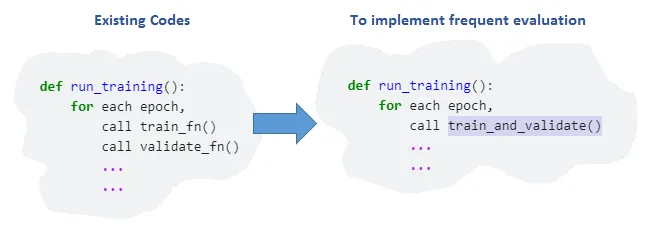
在train_and_validate内,对于每个批次的训练数据,它将运行模型训练代码。但是,对于验证,validate_fn仅会在每个x批次的训练数据上调用一次。因此,如果x为10,如果我们有50个训练数据批次,则每个时期将进行5次验证。

Results
这些技术能够为结果的大幅提升做出很大的贡献,结果在下表中展示。
使用基本微调的平均RMSE(Root Mean Square Error)得分为0.589,而使用本文介绍的所有高级技术后,平均RMSE得分为0.5199
| Fine-tuning Techniques | Mean RMSE (5-fold CVs) |
|---|---|
| Basic fine-tuning | 0.589 |
| LLRD | 0.575 |
| LLRD (50 warm-up steps) | 0.5717 |
| LLRD (50 warm-up steps) + re-initialize top 5 layers | 0.5543 |
| LLRD (50 warm-up steps) + re-initialize top 5 layers + SWA | 0.5504 |
| LLRD (50 warm-up steps) + re-initialize top 5 layers + SWA + frequent evaluation | 0.5209 |
| Grouped LLRD (50 warm-up steps) + re-initialize top 5 layers + SWA + frequent evaluation | 0.5199 |
Summary
这篇文章介绍了用于微调Transformer的各种技术。
-
我们使用了分层学习率衰减(LLRD)。LLRD背后的主要思想是对Transformer的每个层或层组应用不同的学习率,对于层组,应用不同的学习率。具体来说,顶层应该比底层具有更高的学习率。
-
我们在学习率表中使用了热身步骤。在线性时间表中进行热身步骤,学习率从0线性增加到优化器中设置的初始学习率,在热身阶段之后,它们开始线性减少到0。
-
我们还对Transformer的前n层进行了重新初始化。选择n的最佳值至关重要,因为如果重新初始化超过最佳点的更多层,则可能开始出现恶化的结果。
-
我们应用了随机权重平均(SWA),这是一种使用修改后的学习率表的深度神经网络训练技术。它还在训练时间的最后一段内保持了权重的运行平均值。
-
最后但并非最不重要的是,我们在Transformer微调过程中引入了频繁的评估。我们不是在每个时期都进行一次验证,而是在时期内的每个x批次的训练数据中进行验证。通过所有这些技术,我们看到了结果的巨大改进,如表种数据所示。