摘要
这篇论文研究了BERT上下文表示的微调,重点关注了少样本场景中常见的不稳定性。我们确定了几个导致这种不稳定性的因素:使用具有偏差梯度估计的非标准优化方法;BERT网络的重要部分在下游任务中的适用性有限;以及使用预先确定的、很少的训练迭代次数的普遍做法。我们通过实验证明了这些因素的影响,并确定了解决这一过程中常见不稳定性的替代做法。基于这些观察结果,我们重新审视了最近提出的改进BERT少样本微调方法,并重新评估了它们的有效性。总体而言,我们观察到这些方法的影响随着我们修改后的过程而显著减弱。
1. 介绍
自我监督预训练模型的微调显著提高了自然语言处理(NLP)任务的最新性能(Liu,2019;Yang等,2019a;Wadden等,2019;Zhu等,2020;Guu等,2020)。其中最有效的模型之一是BERT(Devlin等,2019)。然而,尽管取得了显著的成功,但在使用BERTLarge等大型BERT变体处理小数据集时,微调仍然不稳定,其中预训练可以提供最大的好处。使用不同随机种子的相同学习过程通常会导致微调后出现明显不同甚至退化的模型,尽管随机种子只影响学习过程中的一些看似微不足道的方面(Phang等人,2018;Lee等人,2020;Dodge等人,2020)。因此,从业者会进行多次随机试验以进行模型选择。这增加了模型部署成本和时间,并使科学比较具有挑战性(Dodge等人,2020)。
这篇论文是对少样本BERT微调优化过程的不同方面进行研究。我们的目标是更好地理解优化算法、模型初始化和微调训练迭代次数等常见选择对此过程的影响。我们确定了几个导致不稳定性的因素:使用非标准优化器会引入梯度估计偏差;预训练BERT模型的顶层提供了一个不良的微调初始化点;使用预定的、但常用的训练迭代次数会影响收敛。我们通过在多个常见基准测试上进行实验来研究这些问题及其解决方法,重点关注少样本微调场景。
一旦解决了这些次优实践,我们观察到退化的运行被消除,性能变得更加稳定。这使得不必执行Dodge等人提出的大量随机重启。我们的实验表明,我们为每个问题实验的疗法具有重叠效应。例如,分配更多的训练迭代次数最终可以补偿使用非标准偏差优化器,即使偏差校正优化器和重新初始化一些预训练模型参数的组合可以减少微调计算成本。这从经验上突出了微调不同方面如何影响过程的稳定性,有时以类似的方式。根据我们的观察结果,我们重新评估了几种技术(Phang等人,2018; Lee等人,2020; Howard&Ruder,2018),这些技术最近被提出以增加少量样本微调稳定性,并显示其影响显着减小。我们的工作进一步推动了对微调过程的经验理解,并且我们概述的优化实践确定了未来方法发展的有影响力的途径。
2. 背景和相关工作
BERT: The Bidirectional Encoder Representations from Transformers (BERT; Devlin et al., 2019)是一种双向编码器,它使用掩码语言建模和下一句预测目标在原始文本上进行训练。对于每个输入标记,它生成一个上下文向量,这个向量是通过一堆Transformer块进行上下文化的。BERT在输入句子或句子对之前添加一个特殊的[CLS]标记。这个标记的嵌入被用作分类任务的输入摘要标记。这个嵌入是通过具有tanh非线性的附加全连接层计算的,通常称为汇聚器,以聚合[CLS]嵌入的信息。
Fine-tuning: 使用预训练的BERT模型的常见方法是将原始输出层替换为新的任务特定层并对整个模型进行微调。这包括学习新的输出层参数并修改所有原始权重,包括单词嵌入、变压器块和池化器的权重。例如,对于句子级分类,添加的线性分类器将[CLS]嵌入投影到输出类别上的未归一化概率向量。这个过程引入了两个随机源:新输出层的权重初始化和随机微调优化中的数据顺序。现有工作表明,这些看似良性的因素可以显著影响结果,特别是在小数据集(即<10K个示例)上(Phang等人,2018; Lee等人,2020; Dodge等人,2020)。因此,从业者经常进行多次随机试验以选择基于验证性能的最佳模型(Devlin等人,2019)。
Fine-tuning Instability: BERT的微调过程不稳定性自其推出以来就已经被人们所知(Devlin等人,2019),并且已经提出了各种方法来解决这个问题。Phang等人(2018)表明,在大型中间任务上微调预训练模型可以稳定后续的小数据集微调;Lee等人(2020)引入了一种新的正则化方法,以约束微调模型保持接近预训练权重,并表明它可以稳定微调;Dodge等人(2020)提出了一种早期停止方法,以有效地过滤可能导致性能不佳的随机种子。与我们的工作同时进行的Mosbach等人(2020)也表明,在微调过程中BERTADAM会导致不稳定性。我们的实验研究了训练时间对模型稳定性的影响,这与之前研究从头开始训练模型的问题有关(Popel和Bojar,2018;Nakkiran等人,2019)。
BERT Representation Transferability: BERT预训练表示已广泛使用探测方法进行研究,表明中间层的预训练特征更易于转移(Tenney等人,2019b; a; Liu等人,2019a; Hewitt&Manning,2019; Hewitt&Liang,2019)或适用于新任务(Zhang等人,2020)比后期层的特征更易于转移(Peters等人,2019; Merchant等人,2020)。我们的工作受到这些发现的启发,但侧重于研究预训练权重如何影响微调过程。 Li等人(2020)建议重新初始化ConvNet的最终全连接层,并显示图像分类的性能增益。与我们的工作同时进行,Tamkin等人(2020)采用类似的权重重新初始化方法(第5节)来研究BERT的可转移性。与我们的研究不同,他们的工作强调确定对转移学习做出最大贡献的层以及探测性能和可转移性之间的关系。
3. EXPERIMENTAL METHODOLOGY
Data: 我们遵循先前研究的数据设置(Lee等人,2020;Phang等人,2018;Dodge等人,2020),使用GLUE基准测试(Wang等人,2019b)中的八个数据集来研究少样本微调。这些数据集涵盖四个任务:自然语言推理(RTE、QNLI、MNLI)、释义检测(MRPC、QQP)、情感分类(SST-2)和语言可接受性(CoLA)。附录A提供了数据集统计信息和每个数据集的描述。我们的研究集中在四个数据集(RTE、MRPC、STS-B、CoLA)上,这些数据集的训练样本少于10k,因为已知在这些数据集上进行BERT微调是不稳定的。我们还通过按照Phang等人的方法将所有八个数据集的样本量降至1k来补充我们的研究。我们将保留测试集以进行研究。对于RTE、MRPC、STS-B和CoLA,我们将原始验证集分成两半,其中一半用于验证,另一半用于测试。对于其他四个较大的数据集,我们只研究了降采样版本,并从训练集中分配了额外的1k样本作为验证数据,并在原始验证集上进行测试。
Experimental Setup: 除非另有说明,否则我们遵循Lee等人的超参数设置。我们使用批量大小为32、dropout为0.1、峰值学习率为$2×10^{−5}$的uncased、24层BERTLarge模型进行微调,微调3个时期。我们将梯度剪裁为最大范数为1。我们在前10%的更新期间应用线性学习率预热,然后进行线性衰减。我们使用Apex4进行混合精度训练以加速实验。我们在附录C中展示了混合精度训练不会影响微调性能。我们在训练期间对验证集进行了十次评估,并进行了早期停止。我们使用20个随机种子进行微调,以比较不同的设置。
4. OPTIMIZATION ALGORITHM: DEBIASING OMISSION IN BERTADAM
BERT的微调最常用的优化器是BERTADAM,这是ADAM一阶随机优化方法的修改版本。它与原始的ADAM算法(Kingma和Ba,2014)不同,因为它省略了偏差校正步骤。这个变化是由Devlin等人引入的(2019),随后被纳入了常见的开源库中,包括官方实现、huggingface的Transformers、AllenNLP、GluonNLP、jiant、MT-DNN和FARM。因此,这个非标准实现在工业和研究中被广泛使用。我们观察到,偏差校正的省略会影响学习率,特别是在微调BERT的早期阶段,并且是导致BERT微调不稳定的主要原因之一(Devlin等人,2019;Phang等人,2018;Lee等人,2020;Dodge等人,2020)。
Algorithm 1: 自Kingma和Ba(2014)调整的ADAM伪代码,仅供参考。$g^2_t$表示元素平方$g_t \odot g_t$。$β_1$和$β_2$的t次方表示为$β^t_1β^t_2$。向量上的所有操作都是逐元素的。根据Kingma和Ba(2014)的建议,超参数值为:$α = 0.001$,$β_1 = 0.9$,$β_2 = 0.999$和$ε = 10^{−8}$。BERTADAM(Devlin等人,2019)省略了偏差校正(第9-10行),并将$m_t$和$v_t$视为$\hat m_t$和$\hat v_t$(第11行)。
Require: α: learning rate; $β_1, β_2 ∈ [0, 1)$: exponential decay rates for the moment estimates; $f(θ)$: stochastic
objective function with parameters $θ$; $θ_0$: initial parameter vector; $λ ∈ [0, 1)$: decoupled weight decay.
1: $m_0 ← 0$ (Initialize first moment vector)
2: $v_0 ← 0$ (Initialize second moment vector)
3: $t ← 0$ (Initialize timestep)
4: while $θ_t$ not converged do
5: $t ← t + 1$
6: $g_t ← ∇θ f_t(θ{t−1})$ (Get gradients w.r.t. stochastic objective at timestep t)
7: $m_t ← β_1 · m_{t−1} + (1 − β_1) · g_t$ (Update biased first moment estimate)
8: $v_t ← β_2 · v_{t−1} + (1 − β_2) · g^2_t$ (Update biased second raw moment estimate)
9: $\hat m_t ← m_t/(1 − β^t_1) $ (Compute bias-corrected first moment estimate)
10: $\hat v_t ← v_t/(1 − β^t_2) $ (Compute bias-corrected second raw moment estimate)
11: $θ_t ← θ_{t−1}− α · \hat m_t/{(\sqrt{\hat v_t }+ \epsilon)}$ (Update parameters)
12: end while
13: return $θ_t$ (Resulting parameters)
算法1显示了ADAM算法,并突出显示了非标准BERTADAM实现中省略的行。 在每个优化步骤(第4-11行)中,ADAM计算梯度($m_t$)和平方梯度($v_t$)的指数移动平均值,其中$β_1$、$β_2$参数化平均值(第7-8行)。由于ADAM将$m_t$和$v_t$初始化为0,并将指数衰减率$β_1$和$β_2$设置接近1,因此在学习早期(t较小时),$m_t$和$v_t$的估计值严重偏向0。Kingma&Ba(2014)计算$m_t$和$v_t$的有偏和无偏估计之间的比率为$(1-β^t_1)$和$(1-β^t_2)$。该比率与训练数据无关。模型参数$θ$沿着平均梯度mt除以第二个矩$\sqrt{v_t}$的方向进行更新(第11行)。BERTADAM省略了去偏差(第9-10行),并直接在参数更新中使用有偏估计。
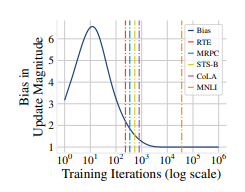
图1 ;ADAM更新的偏差随着训练迭代次数的增加而增加。垂直线表示在四个小数据集和一个大数据集(MNLI)上微调BERT所使用的典型迭代次数。小数据集使用较少的迭代次数,受影响最大。
图1显示了使用有偏和无偏估计的更新之间的比率${\hat m_t}/\sqrt {\hat v_t}$作为训练迭代次数的函数。偏差在学习早期相对较高,表明存在过度估计。最终它会收敛到1,这表明当训练足够的迭代次数时,估计偏差将不会产生显著影响。因此,在学习早期,偏差比项对于抵消$m_t$和$v_t$在早期迭代期间的过度估计是最重要的。在实践中,ADAM通过$\frac{\sqrt{1−β^t_2}}{1−β^t_1}$来自适应地重新缩放学习率。这个校正对于使用少于1k次迭代(Devlin等人,2019)进行微调的小数据集上的BERT微调非常重要,因为它们通常使用少于10k个训练样本进行微调。该图显示了RTE、MRPC、STS-B、CoLA和MNLI的训练迭代次数。MNLI是这组数据集中唯一具有大量监督训练示例的数据集。对于小数据集,整个微调过程中偏差比显着高于1,这意味着这些数据集在更新幅度上受到严重过度估计的影响。相比之下,对于MNLI,大部分微调发生在偏差比已经收敛到1的区域内。这就解释了为什么在MNLI上进行微调是相对稳定的(Devlin等人,2019)。
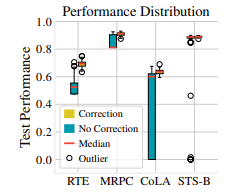
图2 ;展示了50个随机试验的性能分布箱形图,以及四个数据集的ADAM偏差校正前后的结果。可以看到,偏差校正大大降低了微调结果的方差。
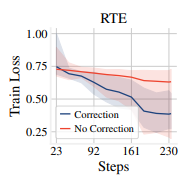
图3 ;在50个随机试验中,微调BERT期间训练损失的平均值(实线)和范围(阴影区域)。偏差校正加速了收敛并缩小了训练损失的范围。
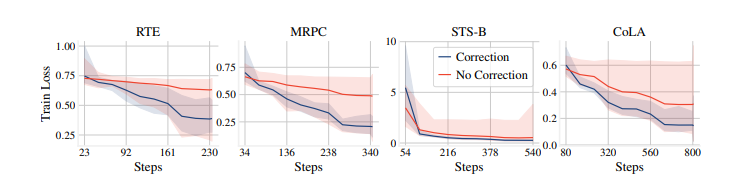
图11 ;训练 BERT 过程中的训练损失的平均值(实线)和范围(阴影区域)在 50 次随机试验中的变化。偏差校正加速了收敛并减小了训练损失的范围。
我们通过在RTE、MRPC、STS-B和CoLA上使用BERTADAM和去偏置的ADAM对BERT进行微调的50个随机种子进行评估,经验地评估了去偏置步骤的重要性。图2总结了性能分布。偏差校正显着降低了不同随机试验和四个数据集之间的性能方差。没有偏差校正,我们观察到许多退化运行,其中微调模型未能优于随机基线。例如,在RTE上,48%的微调运行的准确率低于55%,接近随机猜测。图3进一步说明了这种差异,通过绘制在RTE上不同随机试验期间的训练损失的平均值和范围。附录F中的图11显示了MRPC、STS-B和CoLA的类似情况。有偏见的BERTADAM始终导致更差的平均训练损失,并且在所有数据集上都导致更高的最大训练损失。这表明使用BERTAdam训练的模型欠拟合,不稳定性的根源在于优化。
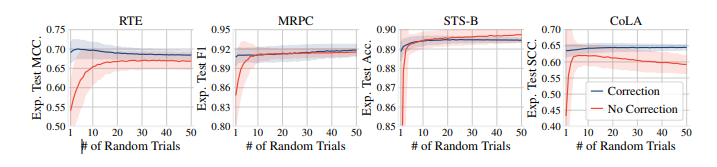
图4 ;在为BERT微调分配的随机试验次数上,预期测试性能(实线)与标准差(阴影区域)。通过偏差校正,我们可靠地在少量(即5或10)次随机试验中获得良好的结果。
我们模拟了多次随机试验的真实情况,遵循 Dodge et al. (2020)。我们使用自助法进行模拟:给定我们训练的 50 个微调模型,我们进行有放回地抽样,对验证集进行模型选择,并记录测试结果;我们重复这个过程 1k 次以估计均值和方差。图 4 显示了模拟测试结果与随机试验次数的关系。附录 E 提供了相同的验证性能图。使用去偏 ADAM,我们可以可靠地使用较少的随机试验来获得良好的结果;当我们进行少于 10 次试验时,预期性能的差异尤为显著。虽然预期验证性能随着更多随机试验而单调提高(Dodge et al.,2020),但当我们进行太多随机试验时,预期测试性能会恶化,因为模型选择过程可能会过度拟合验证集。基于这些观察结果,我们建议进行适度数量的随机试验(即 5 或 10)。
5. INITIALIZATION: RE-INITIALIZING BERT PRE-TRAINED LAYERS
神经网络的初始参数对深度神经网络的训练过程有重要影响,因此存在各种方法来进行谨慎的初始化(Glorot&Bengio,2010;He等,2015;Zhang等,2019;Radford等,2019;Dauphin&Schoenholz,2019)。在微调期间,BERT参数扮演了微调优化过程的初始化点的角色,同时还捕获了从预训练中传输的信息。 BERT微调的常见方法是使用预训练权重初始化除一个专门输出层以外的所有层。我们研究了将所有层传输到简单忽略某些层中学到的信息之间的价值。这是由目标识别转移学习结果驱动的,显示出较低的预训练层学习更通用的特征,而更接近输出的更高层更专注于预训练任务(Yosinski等人,2014)。使用BERT的现有方法表明,使用完整网络并不总是最有效的选择,我们在第2节中进行了讨论。我们的实证结果进一步证实了这一点:我们观察到传输顶部预训练层会减慢学习速度并损害性能。
我们测试了使用简单的消融研究来测试顶层的可转移性。我们重新初始化了池化器层和顶部$L∈N$ BERT Transformer块,使用原始BERT初始化,$N(0,0.02^2)$。我们比较了两种设置:(a)使用BERT进行标准微调,(b)重新初始化BERT的微调。我们通过选择$L∈{1,…,6}$来评估Re-init,该选择基于平均验证性能。所有实验都使用具有20个随机种子的去偏置ADAM(第4节)。
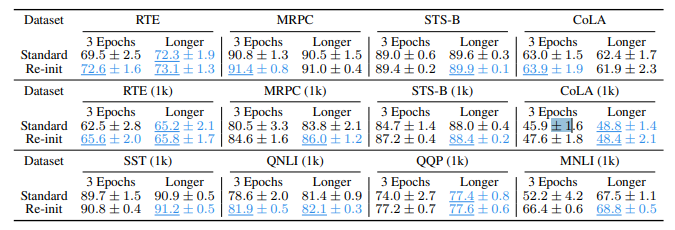
表1 ;平均测试性能和标准差。我们比较使用完整BERT模型(标准)进行微调和使用部分重新初始化的BERT(Re-init)进行微调。我们展示了微调3个时期和更长时间的结果(第6节)。我们在每组4个数字中下划线和用蓝色突出显示最佳数字及与其在统计上等效的数字。我们使用单一样本t检验,当p <0.05时拒绝零假设。
重新初始化对性能的影响: 表1显示了我们在第3节中所有数据集上的结果。我们展示了使用3个epoch的常见设置的结果,以及在第6节中讨论和研究的更长时间的训练。重新初始化始终提高所有数据集上的平均性能,表明并非所有层都有助于转移。它通常还会减少所有数据集上的方差。附录F显示了BERT以外的预训练模型类似的好处。
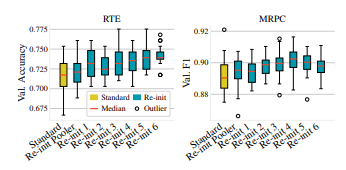
图5 ;重新初始化BERT模型的不同层数的验证性能分布
重新初始化的层数对灵敏度的影响: 图5显示了我们重新初始化的块数L对RTE和MRPC的影响。附录F中的图13显示了其他数据集的类似情况。我们观察到最坏情况下的性能改善比最佳性能更显著,这表明Re-init对不利的随机种子更具有鲁棒性。当仅重新初始化pooler层时,我们已经看到了改进。重新初始化更多层会更有帮助。对于较大的L,性能会趋于平稳甚至下降,因为重新初始化具有重要通用特征的预训练层。最佳L因数据集而异。
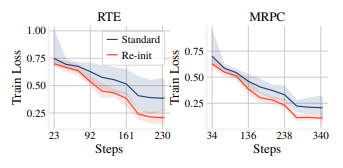
图6 ;BERT 微调期间训练损失的平均值(实线)和范围(阴影区域),在 20 次随机试验中。重新初始化导致更快的收敛并缩小了范围。
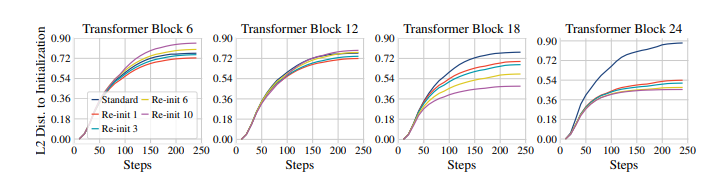
图7 ;在RTE上微调BERT时与初始参数的L2距离。重新初始化减少了顶部Transformer块的权重变化量。但是,重新初始化太多层会导致底部Transformer块的变化更大。
收敛效果和参数变化的影响: 图6显示了标准微调和RTE、MRPC上的重新初始化的训练损失。附录F的图13显示了所有其他数据集的训练损失。重新初始化导致更快的收敛。我们研究了不同Transformer块的权重。对于每个块,我们将所有参数连接起来,并记录微调期间这些参数及其初始化值之间的L2距离。图7以RTE上的训练步骤为函数绘制了四个不同变压器块的L2距离,附录F中的图15-18显示了四个数据集上的所有变压器块。总体而言,重新初始化减小了顶部Transformer块(即18-24)的L2距离。重新初始化更多层会导致更大的减少,表明重新初始化减少了微调工作量。 Re-init的效果不是局部的;即使仅重新初始化最顶层的Transformer块,也会影响整个网络。虽然设置L = 1或L = 3仍有利于底部Transformer块,但重新初始化太多层(例如L = 10)可能会增加底部Transformer块中的L2距离,表明底部和顶部Transformer块之间存在权衡。总之,这些结果表明Re-init找到了更好的微调初始化,并且BERT的顶部L层可能过于专门化于预训练目标。
6. TRAINING ITERATIONS: FINE-TUNING BERT FOR LONGERBERT
通常使用倾斜三角形学习率进行微调,该学习率应用线性预热到学习率,然后进行线性衰减。这种学习计划需要事先决定训练迭代次数。Devlin等人(2019)建议将GLUE数据集进行微调三个时期。这个建议已经广泛用于微调(Phang等人,2018; Lee等人,2020; Dodge等人,2020)。我们研究了这种选择的影响,并观察到BERT微调的这种一刀切的三个时期做法是次优的。微调BERT时间更长可以提高训练稳定性和模型性能。
Experimental setup: 我们研究了在第3节中的数据集上增加微调迭代次数的影响。对于1k下采样的数据集,其中三个时期对应96个步骤,我们在{200、400、800、1600、3200}中调整迭代次数。对于四个小数据集,我们在相同范围内调整迭代次数,但跳过小于三个时期使用的迭代次数的值。在微调过程中,我们在验证集上对模型进行了10次评估。这个数字与第4-5节的实验相同,并控制了要选择的模型集。我们使用8个不同的随机种子进行调整,并根据平均验证性能选择最佳的超参数集以节省实验成本。在超参数搜索之后,我们使用最佳超参数对20个种子进行微调,并报告测试性能。
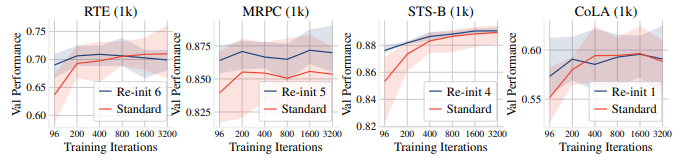
图8 ;不同迭代次数下,八个随机试验的验证性能的平均值(实线)和范围(阴影区)
Results: 表1显示了Longer列下的结果。在大多数情况下,训练时间更长可以提高性能和稳定性,尤其是在1k下采样的数据集上。我们还发现,训练时间更长可以减少标准微调和Re-init之间的差距,表明训练更多次可以帮助这些模型从不良初始化中恢复过来。但是,在MRPC和MNLI等数据集上,即使训练时间更长,Re-init仍然可以提高最终性能。我们在Figure 8中显示了四个下采样数据集的验证结果,这些数据集具有不同数量的训练迭代次数。我们在附录G的Figure 14中提供了类似的图形,用于其他下采样数据集。我们观察到,不同的任务通常需要不同数量的训练迭代次数,很难找到一种适合所有情况的解决方案。因此,我们建议从业者在微调中发现不稳定性时,在其数据集上调整训练迭代次数。我们还观察到,在大多数数据集上,Re-init需要更少的迭代次数才能达到最佳性能,这证实了Re-init为微调提供了更好的初始化。
7. REVISITING EXISTING METHODS FOR FEW-SAMPLE BERT FINE-TUNING
BERT 微调不稳定,特别是在少样本情况下,最近受到越来越多的关注(Devlin等人,2019;Phang等人,2018;Lee等人,2020;Dodge等人,2020)。我们重新审视了这些方法,考虑使用去偏置的ADAM代替BERTADAM的影响(第4节)。一般来说,我们发现当这些方法使用无偏ADAM重新评估时,它们在微调稳定性和性能方面的改进效果较小。
7.1 OVERVIEW
Pre-trained Weight Decay: 权重衰减(Weight decay,WD)是一种常见的正则化技术(Krogh & Hertz,1992)。在每次优化迭代中,从模型参数中减去$λw$,其中λ是正则化强度的超参数,$w$是模型参数。预训练权重衰减将此方法用于微调预训练模型(Chelba & Acero,2004;Daumé III,2007),通过从目标中减去$λ(w-\hat w)$,其中$\hat w$是预训练参数。Lee等人(2020)实验证明,在BERT微调中,预训练权重衰减比传统的权重衰减效果更好,并且可以稳定微调。
Mixout: Mixout是一种随机正则化技术,受Dropout和DropConnect的启发。在每个训练迭代中,每个模型参数都有概率$p$被替换为其预训练值。目的是防止灾难性遗忘,并且证明它可以约束微调模型不会偏离预训练初始化。
Layer-wise Learning Rate Decay (LLRD): 层间学习率衰减(LLRD)是一种方法,它为顶层应用更高的学习率,为底层应用更低的学习率。这是通过设置顶层的学习率并使用一个乘性衰减率从顶部到底部逐层降低学习率来实现的。其目的是比较少修改编码更一般信息的较低层,而更多修改与预训练任务更相关的顶层。这种方法被用于微调最近几个预训练模型,包括XLNet和ELECTRA。
Transferring via an Intermediate Task(通过中间任务转移): Phang等人(2018)建议在少样本数据集上进行微调之前,在较大的中间任务上进行补充微调。他们表明,这种方法可以减少不同随机试验之间的方差并提高模型性能。他们的结果表明,将在MNLI(Williams等人,2018)上微调的模型转移后,可以显着提高多个下游任务的性能,包括RTE、MRPC和STS-B。与其他方法相比,这种方法需要大量的额外注释数据。
7.2 EXPERIMENTS
我们在RTE、MRPC、STS-B和CoLA上评估了所有方法。我们使用ADAM优化器和去偏差进行三个时期的BERTLarge模型微调,这是每种方法使用的默认时期数。对于中间任务微调,我们在MNLI上微调BERTLarge模型,然后进行评估微调。对于其他方法,我们为每种方法使用类似大小的搜索空间进行超参数搜索,如附录H所述。我们使用20个随机种子的平均验证性能进行模型选择。我们还报告了标准微调的结果,包括更长的训练时间(第6节),权重衰减和重新初始化(第5节)。

表2 ; 四个数据集上的平均测试性能和标准偏差。比标准设置(左列)显著更好的数字以蓝色和下划线表示。 Re-init和Longer的结果从表1复制而来。所有实验都使用带有去偏差的ADAM(第4节)。除了Longer之外,所有方法都使用三个时期进行训练。 “Int. Task”代表通过中间任务(MNLI)进行转移。
表格2提供了我们的结果。与已发表的结果(Phang等人,2018; Lee等人,2020)相比, 我们使用ADAM进行去偏差时,通过中间任务(通过中间任务进行转移),Mixout,预训练 WD和WD的测试性能通常更高。但是,与最初报告的结果相比,我们观察到所有调查方法的 效益不太明显。有时,这些方法并不优于标准基线或仅仅是训练时间更长。使用附加注释数据 进行中间任务训练仍然是有效的,可以在所有数据集上提高平均性能。 LLRD和Mixout的性能影响 较小。我们在实验中观察到,在改进或稳定BERT微调方面使用预训练权重衰减和传统权重衰减 没有明显的改进,这与现有工作(Lee等人,2020)相反。这表明这些方法可能会缓解BERTADAM中 去偏差遗漏带来的优化困难,在我们添加去偏差时,积极影响会减少。
8. CONCLUSION
我们已经证明了优化在少样本BERT微调中发挥了至关重要的作用。首先,我们表明BERTADAM中的去偏差省略是导致在小数据集上常见的退化模型的主要原因(Phang等人,2018; Lee等人,2020; Dodge等人,2020)。其次,我们观察到预训练BERT的顶层提供了对微调和延迟学习有害的初始化。简单地重新初始化这些层不仅可以加速学习,而且可以提高模型性能。第三,我们证明了BERT微调的常见一刀切三个时期的做法是次优的,分配更多的训练时间可以稳定微调。最后,我们重新审视了几种用于稳定BERT微调的方法,并观察到它们的正面效果随着去偏差ADAM而减弱。在未来,我们计划将研究扩展到不同的预训练目标和模型架构,并研究模型参数在微调过程中如何演变。
附录
A. DATASETS
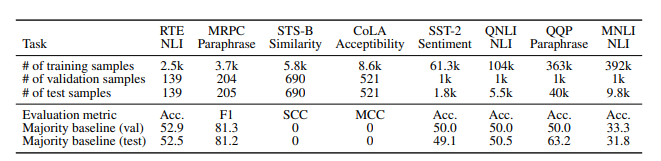
表3 ; 这项工作中使用的数据集。我们应用非标准数据拆分来创建测试集。SCC代表Spearman相关系数,MCC代表Matthews相关系数。
Table 3总结了数据集的统计信息,并描述了我们的验证/测试拆分。我们还为每个数据集提供了简要介绍:
RTE 文本蕴含识别(Bentivogli等人,2009)是一个二元蕴含分类任务。我们使用GLUE版本。
MRPC Microsoft Research Paraphrase Corpus(Dolan&Brockett,2005)是二元分类任务。给定一对句子,模型必须预测它们是否是彼此的释义。我们使用GLUE版本。
STS-B 语义文本相似性基准(Cer等人,2017)是用于估计一对句子之间的句子相似度的回归任务。我们使用GLUE版本。
CoLA 语言可接受性语料库(Warstadt等人,2019)是用于验证一系列单词是否为语法正确的英语句子的二元分类任务。使用Matthews相关系数(Matthews,1975)来评估性能。我们使用GLUE版本。
MNLI 多种类型自然语言推理语料库(Williams等人,2018)是一个文本蕴含数据集,其中要求模型预测前提是否蕴含假设,预测假设或两者都不是。我们使用GLUE版本。
QQP Quora问题对(Iyer等人,2017)是一个二元分类任务,用于确定两个问题是否在语义上等效(即是否互为释义)。我们使用GLUE版本。
SST-2 斯坦福情感树库的二元版本(Socher等人,2013)是一个二元分类任务,用于判断句子是否具有积极或消极情感。我们使用GLUE版本。